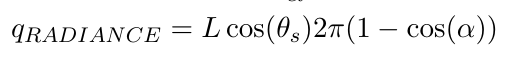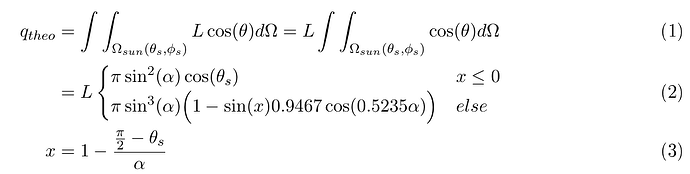Hi all,
I am currently carrying out an investigation of a simple scene. To do this, I place a sensor at {0,0,0} with upward orientation {0,0,1}. There is no other material, ground or other surfaces in the scene. Now I create 10000 “void light” surfaces with a radiance of 1.5e7 and a fixed angle alpha. The “light” material primitives are equally distributed from a zenith angle of 0 to 90°. The azimuth angle is always 0. I then weight all channels with {1/3,1/3,1/3}. This is an open scene so rcontrib does no bounce (-ab 0). Those are the other settings (-I+ -V+ -ab 0 -y 2 -t 5 -dc 1 -dt 0 -dj 0).
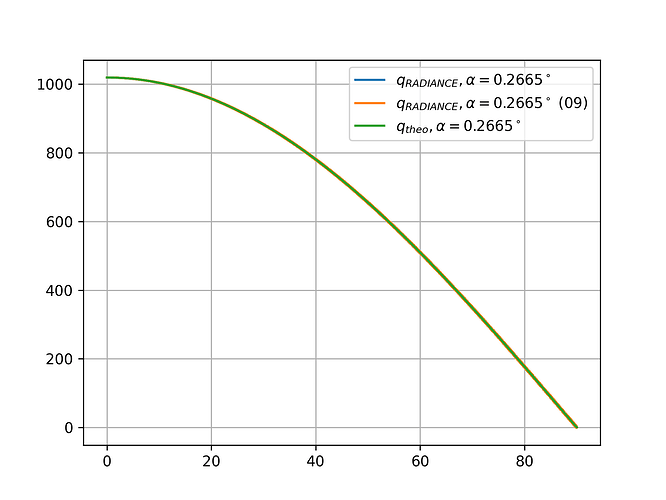
Theoretically, the following relationship should result.
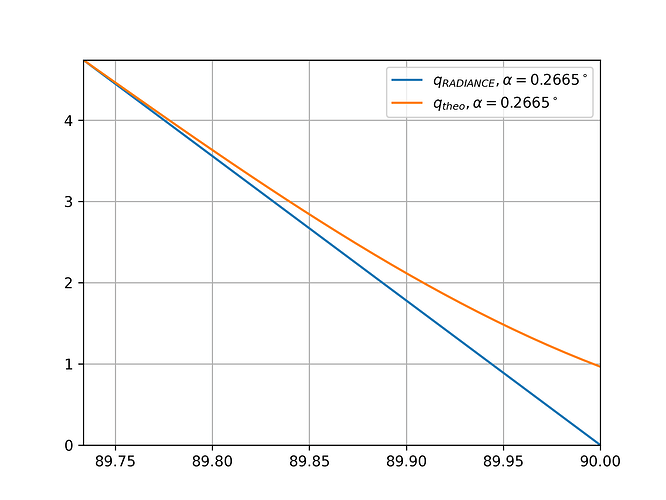
This is what RADIANCE gives me back.
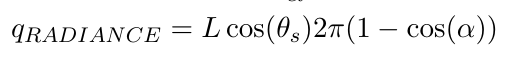
First of all i compared the results for alpha=0.2665°, so the classical half angle of the sun disc.
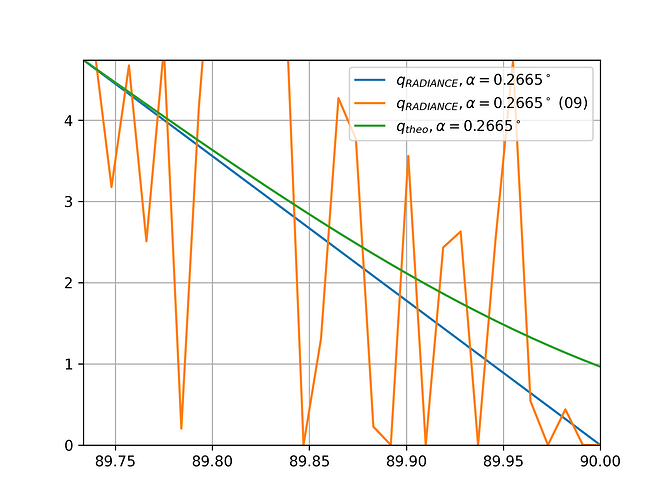
I seems like everything is fine, until we zoom in.
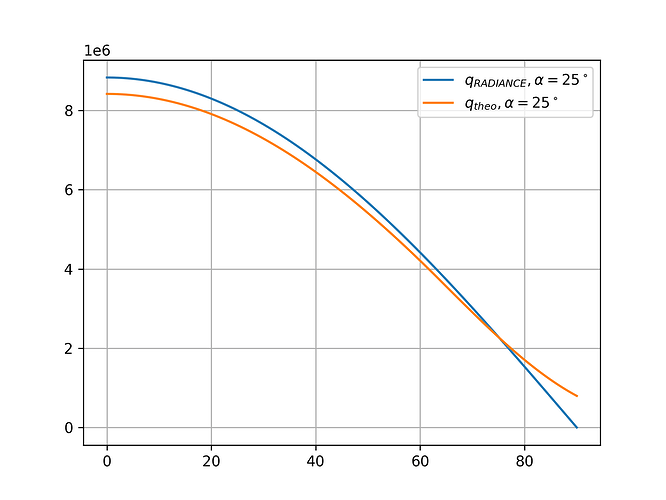
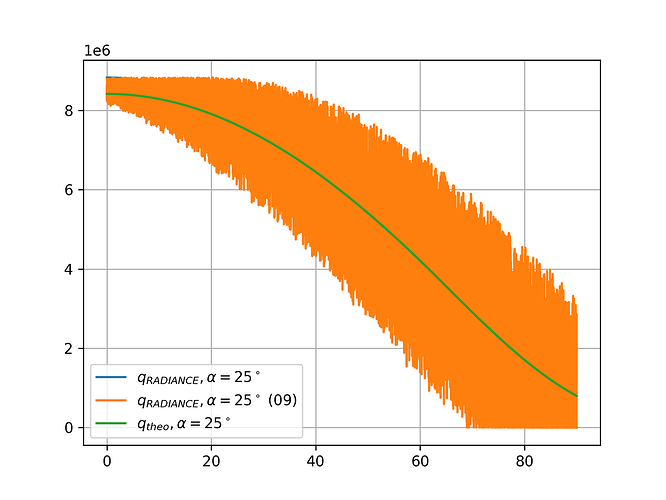
Additionally, I did the same with a half angle of 25°. Thats the half angle for the simplified Perez Sky model.
The deviations are much higher for that half angle.
So my questions are:
- Why does rcontrib with the light primitive not integrate on the solid angle defined but only evaluating the sun in the disc center?
- Is there a possibility to get to the integrated value?
Kind regards
Simon Weber, M.Sc.
Research Associate
Institute for Acoustics and Building Physics
Pfaffenwaldring 7
70569 Stuttgart
Germany
Tel: +49 711 685 66301
E-Mail: [email protected]
Website: http://www.iabp.uni-stuttgart.de
ORCID
Hi Simon,
This seems a very nice analysis, though I didn’t have time to go over the math. (I am recovering rather too slowly from a bout of the flu and my brain is foggier than usual.)
I suspect the problem is your setting of -dj 0. The default rcontrib setting of -dj .9 would get closer to the correct integrated value, though it won’t be an exact match, either. The “direct” calculation in Radiance is optimized for speed over perfect accuracy. Typically, distributing direct rays randomly over each surface gets a better integral in the presence of penumbras (partial shading), so this is preferred to a numerical integration of source position times cosine. Also, the integral becomes rather too complex when non-diffuse reflectances are involved.
Cheers,
-Greg
Hi Greg,
Thank you very much for your rapid feedback.
I have tried it with the attribute -dj 0.9.
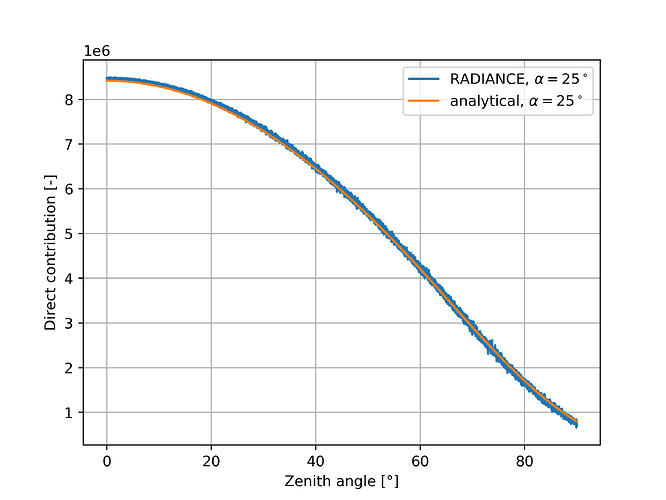
Now there are quite some fluctuations, especially for the simulations with a half angle of 25°.
These are the new plots.
How else could I solve the problem?
In any case, I wish you a speedy recovery.
kr
Simon
Oh, I forgot to mention – you should use the rcontrib -c option, maybe a value of 1000 or so, and send as many duplicate samples as you set. That way, you’ll get an averaged (integrated) result rather than a random sampling.
-Greg
1 Like
Hi Greg,
this is the total directive:
rcontrib -I+ -V+ -ab 0 -y 2 -t 5 -dc 1 -dt 0 -dj 0.9 -faa -M ./sunNames.txt ./scene.oct < ./points.txt > ./dirSun.mtx
Where do i have to place the -c 1000 option? Do i have to remove something instead? Because it doesnt work when I simply place it at after -dj 0.9 for example.
kr Simon
Well, you first need to reproduce each point in your file 1000 times, then add the -c 1000 option to rcontrib. So, assuming you have one point per line, you can use:
repeatlines 1000 < points.txt | rcontrib -c 1000 -I+ -V+ -ab 0 -y 2 -t 5 -dc 1 -dt 0 -dj 0.9 -faa -M ./sunNames.txt scene.oct > dirSun.mtx
Unfortunately, there’s no program called “repeatlines,” so you would need to write one. Here are several options for this.
Best,
-Greg
Hi Greg,
thanks for your suggestion. It worked finally.
I uploaded the raw files under my github account: integralRcontrib/raw at main · weberscode/integralRcontrib · GitHub
2 Likes