Position index below line-of-sight by evalglare

[kikut]

issue

Hello all,
I have been wondering for a long time that evalglare outputs a position index below line-of-sight which is not concentric, while the Einhorn’s equation below looks to draw concentric rings because it depends on only Radius.

posindex = 1 + fact * Radius / D

fact and D, which are respectively a slope factor and a distance from an eye to an image plane, should be constant.

so I tried to fix this issue. could someone give me feedback?

target

in evalglare.c, these 3 lines calculating Radius might cause this issue.

d = 1 / tan(phi);
s = tan(teta) / tan(phi);
r = sqrt(1 / d * 1 / d + s * s / d / d);

changes

this one line will get a correct Radius.

r = tan(sigma/deg);

then, you won’t need these lines placing a cap on Radius.

/*
if (r > 3) {
fact = 1.2;
r = 3;
}
*/

effects

the left distribution is the position index by the current evalglare. the right one is by the fixed evalglare. the upper half is the same.

1. the lower half of the fixed distribution fits the Iwata’s experiment result better.
2. and is concentric as the Einhorn’s equation is.
3. the fixed distribution has less deviation between the upper half and the lower half at the eye level.

[kikut]

as a result of comparison using about 170 indoor scenes I have, the errors don’t seem to be significant unless the scene has larger glare sources located below line of sight.

[Jan_Wienold]

Hi Kikut,
Indeed there is a bug in evalglare (I used the wrong angles for the below line of sight P calculation, based on the original Iwata model) that I realized already in July and that is fixed in the newest version. Iwata and Osterhaus released at CIE2010 an updated version to overcome the inconsistency at the line of sight (phi-angle =0). This solution is even simpler than the original version and ends up with setting the tau angle to 90° below the line of sight and then using the “normal” equation given in the IES lighting handbook. So I made a change in the source-code like this:
if (phi < 0) { tau = 90.0 ; }

However I haven’t released that version yet since I made plenty of other changes/bugfixes (eg. glare source center calculation) and I wanted to be sure that this version evalglare is stable.
As you mentioned, typically the error is quite small.
I still don’t want to release officially this version in the next two/three weeks since I want to do further tests plus some other small changes. But if you are interested I can send you the new version if you volunteer as beta tester - just send me an email to my epfl email account.
Jan
Here how it looks like now:

[kikut]

Hi Jan,
It’s great to get a reply from the developer of DGP!
I’m happy to hear you are going to fix the bug. Some people seem to misunderstand the P distribution from evalglare is true. Evalglare is influential.

that is fixed in the newest version. Iwata and Osterhaus released at CIE2010 an updated version

The CIE2010 version was what I wanted to discuss next. I’m glad that you are going to implement it to evalglare.

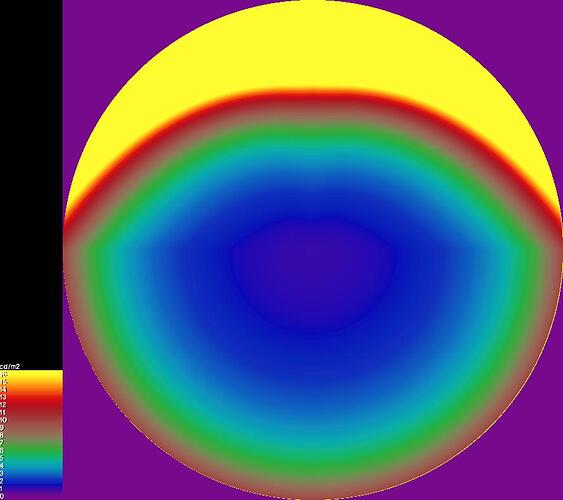
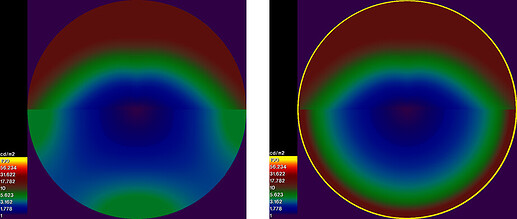
But the image you gave is slightly different from the CIE2010 version, which is not concentric but an ellipse. CIE2010 version is squished vertically.

So I made a change in the source-code like this:
if (phi < 0) { tau = 90.0 ; }

Yes, Iwata mentioned like that and which means at a glance P below line of sight depends on only sigma like this.

posindex = exp(6.49 / 1000 * sigma + 21.0 / 100000 * sigma * sigma);

But it’s a little confusing. (and I guess it might have confused you too.) Iwata continued to mention like this.

sigma = atan⁡[ {x^2+(y*1.15)^2}^0.5/z]

This “sigma” is not the normal sigma in the Guth model. Iwata defines the CIE2010 equation using xyz coordinate system.
So I prefer to replace “sigma” to something which is not duplicate with the existing variables. Let’s call it “beta” for now.

beta = atan⁡[ {x^2+(y*1.15)^2}^0.5/z]

or I prefer to transform the coordinate system to the one using sigma and tau to make it more consistent with Guth model,

beta = atan(tan(sigma)* sqrt(1 + 0.3225 * pow(cos(tau),2)));

These tau and sigma are exactly normal sigma and tau in the Guth model. Both "beta"s are mathematically the same. And then you will get P like this.

posindex = exp(6.49 / 1000 * beta + 21.0 / 100000 * beta * beta);

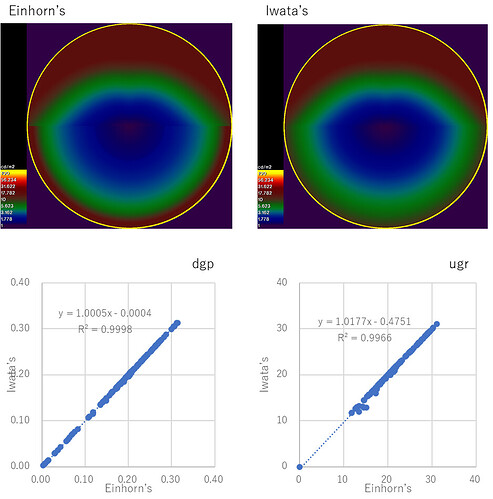
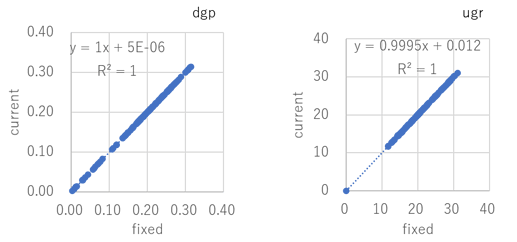
I’ve added the CIE2010 equation into your evalglare.c and got the results below.
It is rounded oval (but hard to tell…) and has a small error when you use it for DGP and UGR unless you have large glare sources below line of sight.

  }if (postype == 2) {
  /* Guth model, equation from IES lighting handbook */
      posindex =
          exp((35.2 - 0.31889 * tau -
              1.22 * exp(-2 * tau / 9)) / 1000 * sigma + (21 +
                                                0.26667 * tau -
                                                0.002963 * tau *
                                                tau) / 100000 *
              sigma * sigma);
  /* below line of sight, using Iwata NEW model */
      if (phi < 0) {
          beta = atan(tan(sigma/deg)* sqrt(1 + 0.3225 * pow(cos(tau/deg),2))) * deg;
          posindex = exp(6.49 / 1000 * beta + 21.0 / 100000 * beta * beta);
      }
    }

Kikuchi