Hello community,
I am back again looking for some help. I’ve been working on generating a sky visibility matrix using Radiance and I’ve partially succeeded. However, I am interesting in learning if there is a more efficient way to use Radiance to do the same thing.
So far, I’ve been using rcontrib and then filtering the resulting daylight coefficients that are larger than zero. This is how my rcontrib call looks like:
rcontrib -n 20 -I+ -faf -ab 0 -y 1 -ad 256 -lw 1.0e-3 -dc 1 -dt 0 -dj 0 -faa -M 9750_suns_modifiers.rad my_scene.oct < my_points.pts
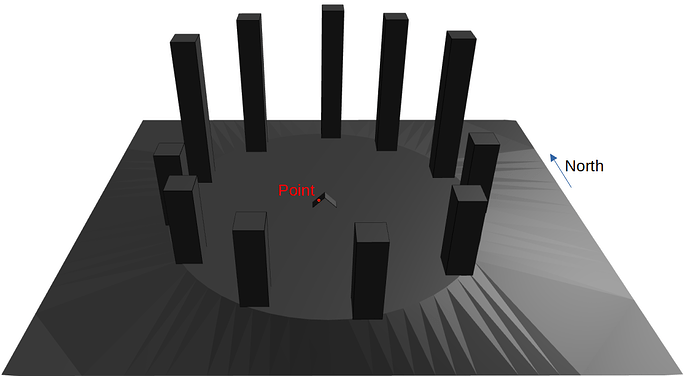
This is how my scene looks like:
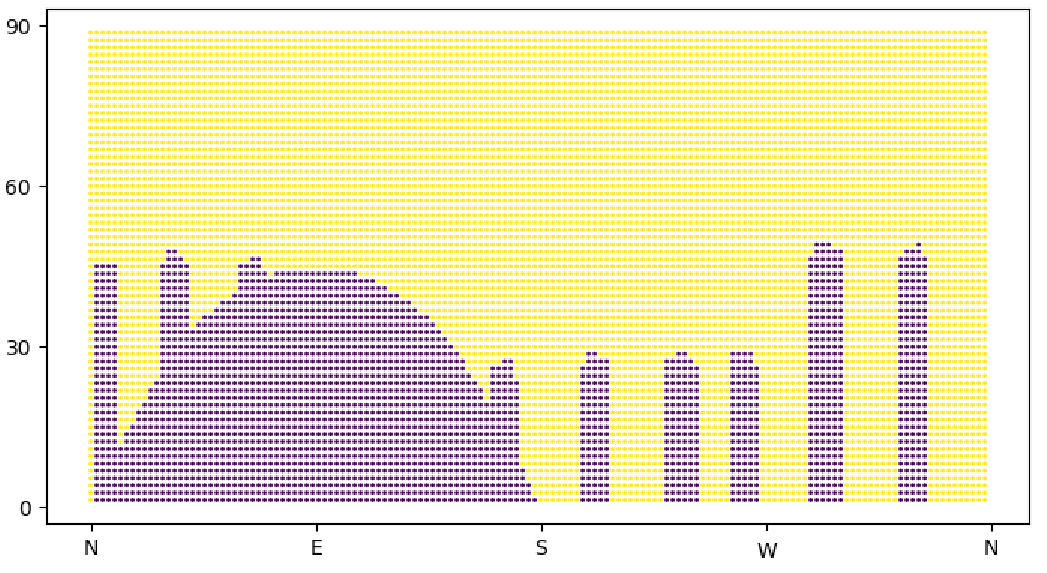
And this is how my result looks like:
I am creating my_scene.oct octree by combining a file that contains a number of plastic polygons (my_scene.rad) and a file that specifies light sources at the positions where I am interested to test the sky visibility:
oconv -f my_scene.rad 9750_suns.rad > my_scene.oct
where my 9750_suns.rad file looks something like this:
void light source_00000 0 0 3 1e6 1e6 1e6
source_00000 source sun_00000 0 0 4 0.00000 0.99972 0.02380 0.533
void light source_00001 0 0 3 1e6 1e6 1e6
source_00001 source sun_00001 0 0 4 0.00000 0.99887 0.04758 0.533
void light source_00002 0 0 3 1e6 1e6 1e6
source_00002 source sun_00002 0 0 4 0.00000 0.99745 0.07134 0.533
…
void light source_09749 0 0 3 1e6 1e6 1e6
source_09749 source sun_09749 0 0 4 -0.00100 0.02378 0.99972 0.533
And my 9750_suns_modifiers.rad file used in the rcontrib call is simply a list of all the modifiers in 9750_suns.rad.
If I understand things correctly, in this case rcontrib simply tests the visibility of each light source with a single ray. If the ray intersects a surface in the octree the result is zero, otherwise, if the light source is visible, the result is the dot product between the normal associated with my test point and the vector pointing to the light source. In my particular case, the actual value of the dot product is not interesting because I am looking for a binary result: visible/not visible.
Given the (relative) simplicity of these calculations, I expected rcontrib to run much faster than it did. Also, it seems like overkill to use a program as powerful as rcontrib to do these simple calculations. So I’m wondering if there’s a more efficient way to achieve the same result.
Does someone have any suggestions?